One of the better software tools available for writing audio effects for microcontrollers is the Teensy Audio Library. It's the thing to use with the Teensy microcontroller, of course, but there's also an Adafruit port that can be used with Adafruit's ATSAMD51-based microcontrollers.
The easy way to get started is to use the graphical design tool to wire together some of the existing components, and let it generate code for you. It's a pretty good tool for beginners, and a great many audio effects can be made that way, but what about writing custom effects that can't be made from the provided components? For that, we'll need to look at the C++ internals of an effect. In this post, I'll walk through writing an effect in C++, using a simple tremolo as an example.
Like most things in C++, an effect consists of two files. In our case, they are:
effect_tremolo.h – a "header" file in which we define the type of the tremolo effect object.
effect_tremolo.cpp – in which we define the functions that will initialize things and calculate the effect's output.
Let's start with effect_tremolo.h. Here's the basic structure of the file, with the details elided for the moment, so you can see the boilerplate that would be about the same (except the names) for any effect:
#ifndef effect_tremolo_h_
#define effect_tremolo_h_
#include "Arduino.h"
#include "AudioStream.h"
class AudioEffectTremolo : public AudioStream
{
...details elided...
};
#endifThe #ifndef, #define and #endif lines are standard C/C++ boilerplate. In another language this would just be the part of the language internals that ensures we don't try to make a new copy of a module every time it's imported, but the creators of C and C++ felt we might enjoy writing this part on our own, every time we create a module.
The #include lines just import some modules that we're going to need.
Then, we get to the point of this file, which is to define the AudioEffectTremolo class, a subclass of AudioStream, which we imported above. Now let's look at the details I elided earlier. There are two main parts, public and private:
class AudioEffectTremolo : public AudioStream
{
public:
AudioEffectTremolo(void):
AudioStream(1, inputQueueArray), position(0) {}
void begin(uint32_t milliseconds);
virtual void update(void);The public part defines the interface of the effect, consisting of three functions: the AudioEffectTremolo constructor that creates an instance of the effect (set up here to be a 1 channel, mono effect), begin, which initializes the effect with its starting values, and update, where the real effect code will happen.
Now for the private part:
private:
audio_block_t *inputQueueArray[1];
// These variables store the current state of the effect.
uint32_t half_cycle_samples;
uint32_t position;
float square_state;
float clickless_sq_state;
float triangle_state;
float parabolic_state; // pseudo-sine wave
};This the internal state of the tremolo effect. Briefly:
inputQueueArray is a block of memory that will receive the input samples to be processed when update is called.
half_cycle_samples is the duration of a half-cycle of the tremolo LFO, expressed as a number of samples. That's a handy form to have it in for the calculations we'll need to do.
position is the current position (that is, sample number) in the tremolo LFO waveform.
The _state variables each hold the latest sample value for one of the waveforms used for the LFO. I'll explain what the "parabolic" thing is all about in a moment.
Okay, header file out of the way, let's get into the main code in effect_tremolo.cpp. First let's look at begin:
// Initialize the tremolo effect with a given speed in milliseconds.
void AudioEffectTremolo::begin(uint32_t milliseconds)
{
// These variables are stored on the AudioEffectTremolo object and
// hold the current state of the effect.
half_cycle_samples = milliseconds * 44.1 / 2.0;
position = 0;
square_state = -1;
clickless_sq_state = -1;
triangle_state = -1;
parabolic_state = 0;
}We take a frequency for the LFO in milliseconds per cycle, and convert it into a number of samples per half-cycle by multiplying by 44.1 (our sample rate is 44100 samples per second, or 44.1 samples per millisecond) and dividing by 2. We also start at position = 0, and start the waveforms at some convenient initial values.
Now let's look at how we do the actual effect, in update. In the file there are a lot of comments explaining what's going on, but I'm removing them here so that we can see the whole thing, and then focus on one thing at a time:
void AudioEffectTremolo::update(void)
{
audio_block_t *block = receiveWritable(0);
if (!block) return;
for (int i = 0; i < AUDIO_BLOCK_SAMPLES; i++) {
if (!(position % half_cycle_samples)) {
square_state = -square_state;
position = 0;
}
if (square_state > clickless_sq_state) {
clickless_sq_state += 0.02;
} else if (square_state < clickless_sq_state) {
clickless_sq_state -= 0.02;
}
clickless_sq_state = constrain(clickless_sq_state, -1, 1);
triangle_state += square_state / (half_cycle_samples / 2);
triangle_state = constrain(triangle_state, -1, 1);
parabolic_state += triangle_state / (half_cycle_samples / 4);
parabolic_state = constrain(parabolic_state, -1, 1);
block->data[i] = block->data[i] * (parabolic_state + 1) / 2;
position++;
}
transmit(block, 0);
release(block);
}At the beginning of the function, we use receiveWritable to get a block of input samples. We'll write over them with our output samples as we work.
At the end of the function, we transmit the output samples on to the next effect in the signal chain, and release the block.
In the middle, we iterate through the input block (AUDIO_BLOCK_SAMPLES is the number of samples it contains), do some calculations to figure out what each output sample should be, and write the new output sample over the input sample at block->data[i].
That pretty much describes how an effect works. The rest of what's going on here is specific to what the tremolo effect does. I'm sure you're curious, so let's go over it:
The basic idea is that we're going to start by keeping the state of a square wave. A square wave just alternates between a high value and a low value every cycle. Because it will be convenient later on, we choose 1 for the high value, and -1 for the low value. The code then switches between those states by keeping track of our current position in the wave (the number of samples processed so far), and flipping the sine of our square_state variable every time the position advances by half_cycle_samples places.
if (!(position % half_cycle_samples)) {
square_state = -square_state;
position = 0;
}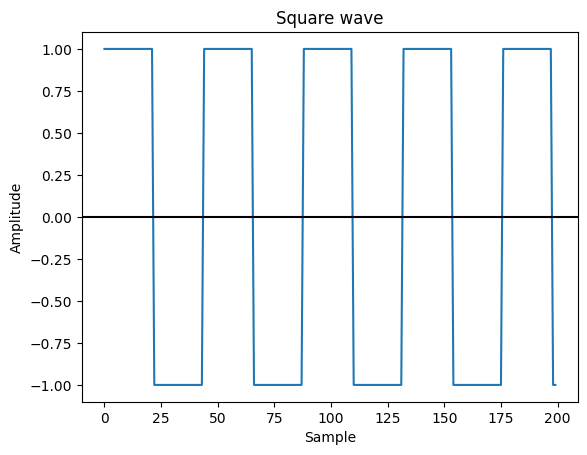
That gives us a square wave. To use it as the LFO waveform for our tremolo, we'll need to use it to turn the volume of the input audio up and down. Here's how we can do that: When the LFO is at 1, we just want to copy the input audio directly to the output, unchanged. When it's at -1, we want to turn the volume all the way down, meaning we'll just send 0 as the value of all the output samples. To make that happen, we can adjust the LFO to range between 1 and 0, and multiply it by the input sample:
// output = input * scaled current LFO value
block->data[i] = block->data[i] * (square_state + 1) / 2;A problem we'll run into if we actually listen to this effect is that those sudden transitions between full volume and silence produce a clicking sound. To eliminate it, we need to transition with a quick fade instead of a sudden jump. That's what clickless_sq_state is all about: instead of jumping suddenly from 0% volume to 100% volume, it goes from 0% to 1%, then 2%, and so on up to 100% over the course of 100 samples (at 44.1 samples per millisecond, that's around two milliseconds, so very quick).
if (square_state > clickless_sq_state) {
clickless_sq_state += 0.02;
} else if (square_state < clickless_sq_state) {
clickless_sq_state -= 0.02;
}
clickless_sq_state = constrain(clickless_sq_state, -1, 1);
That suffices to eliminate the clicks. (By the way, the constrain thing is just to make sure nothing wanders below -1 or above 1 and off toward infinity due to the vagaries of floating point math and discrete approximations.)
Okay, so now we have a square wave LFO. It makes for a fun, choppy, aggressive tremolo. But sometimes you want something a little less harsh and attention-getting. To produce a subtler wobble, we need a smoother waveform. One idea would be to "fade in" half the time by steadily turning the volume up, and then "fade out" by steadily turning it back down. The wave that climbs up in a straight line like that and then back down is called a triangle wave.
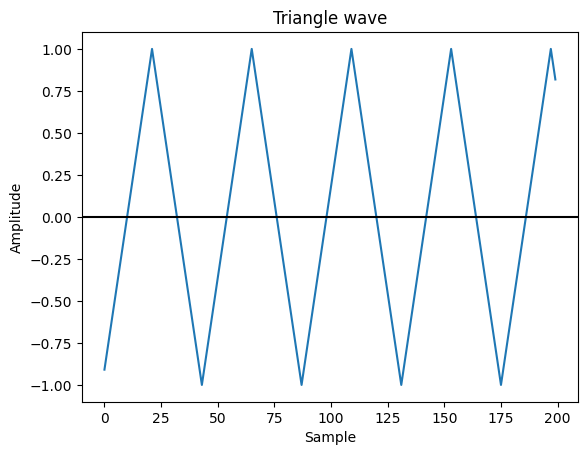
So how do we make a triangle wave? Well, while the square wave is up, we want the triangle wave to be climbing, and while the square wave is down, we want the triangle wave to be falling. If you've done any calculus, you'll recognize this as integration. If not, don't worry about it, the idea is just that the current value of the triangle wave at a given point is the running sum of all the previous values of the square wave up to that point. Let's say we have a square wave that switches states every 3 samples (way too fast, but good for making this example short and easy to read!) Here's how the square wave values would add up:
Square wave value 1, sum 1
Square wave value 1, sum 2
Square wave value 1, sum 3
Square wave value -1, sum 2
Square wave value -1, sum 1
Square wave value -1, sum 0
Square wave value 1, sum 1
...As you can see, while the square wave alternates between two values, its sum climbs by 1 each sample, then drops back down by 1 each sample. You'll also notice that it climbs up to 3 and down to 0, but the shape is what matters here. We can just scale it to 1 to -1 (and later 1 to 0) as needed.
triangle_state += square_state / (half_cycle_samples / 2);
triangle_state = constrain(triangle_state, -1, 1);
Then we can just produce the output the same way as before, multiplying input samples by a scaled triangle wave to ramp the volume up and down.
Finally, an even smoother tremolo wobble would be a sine wave. Getting a true sine wave requires π and trig functions and takes some work to pull off in a way that performs well on a microcontroller. Fortunately, for something like a tremolo a perfect sine wave isn't really necessary, we just want something roughly sine-like, and the wave we can get by integrating the triangle wave will do just fine. Where a triangle wave is made of straight lines, its integral is more of an x² type of thing. It's a bunch of parabolas stitched together, so I'm going to call it a "parabolic wave".
So, we integrate (or, just sum) and scale the square wave to get a triangle wave, and we integrate and scale the triangle wave to get a parabolic wave:
parabolic_state += triangle_state / (half_cycle_samples / 4);
parabolic_state = constrain(parabolic_state, -1, 1);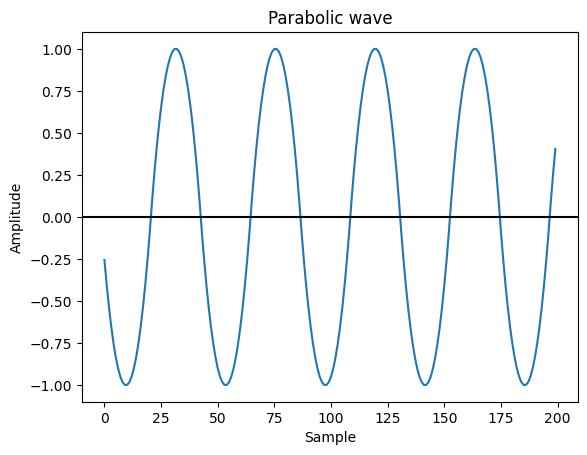
It looks a lot like a sine wave, doesn't it? Close enough for our needs. And now we have a few useful LFO waveforms for a tremolo effect!
Of course, it's worth pointing out that all of this can also be done by just wiring together the effects already provided by the Audio library (waveform and multiply would be the ones to use). Getting into C++ internals like this is only really necessary when you want to do something that can't be made from those components. But now that we've explored how to do it, some of those possibilities should be easier to reach.
You can find the complete code for the tremolo effect here: https://github.com/sah/tremolo